Find the derivatives of Y = ( X +5 )( X2 - 6X )

Find the derivatives of Y = (X +5)(X² - 6X)

SOLUTION

Y = (X +5)(X² - 6X)

Applying the product rule of Indices

dy dx = Udv dx + Vdu dx

Where, U = X+5 and V = X²-6X

So therefore, du dx = 1 and dv dx = 2X-6

Therefore: dy dx = (X+5)(2X-6) + (X² - 6X)1

Lets expand the bracket.

(X+5)(2X-6) = X(2X-6)+5(2X-6)

2X²-6X+10X -30

2X²+4X-30

3X² - 2X - 30

So Therefore, dy dx = 3X²-2X-30

Find the derivatives of Y = 8X4 + 16X3 - 4X2 + X - 20

Question 1 :Y = 8X⁴ + 16X³ - 4X² + X - 20

SOLUTION

Y = 8X⁴ + 16X³ - 4X² + X - 20

Recall that Xⁿ = nX^n-1

So therefore: dy dx = 4(8)X^4-1 + 3(16)X^3-1 - 2(4)X^2-1 + X^1-1 - 0

dy dx = 32X³ + 48X² - 8X + 1

WAEC Mathematics Question 2015 ( Essay Question Seven 7)

QUESTION 7

The table is for the relation 

(a)(i) Use the table to find the values of p and q.

(ii) Copy and complete the table.

(b) Using scales of 2cm to 1 unit on the x- axis and 2 cm to 5 units on the y- axis, draw the graph of the relation for −3≤x≤5$-3\le x\le 5$.

(c) Use the graph to find : 

(i) y when x = 1.8  ; (ii) x when y = -8.

SOLUTION

a(i) To find the value of p and q from the given table of values when x = -3, y= 21

and when x = 4, y = 0.

So considering s = -3 and y = 21 using the givem equation .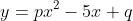

Substituting the vale of x and y  into the equation, we have;

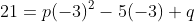
21 =9p + 15 +q

21-15 = 9p + q

6 = 9p +q

9p +q = 6...................... (i)

Also, when x = 4 and y = 0

Substituting into the equation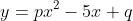 

Substituting the vale of x and y  into the equation, we have;

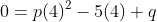
0 = 16p - 20 + q

0 + 20 = 16p + q

20 = 16p + q

16p + q = 20 .......................(ii)

Solving equation (i) and (ii) simultaneously ,

6 = 9p +q ......................... (i)

20 = 16p + q.....................(ii)

9p +q = 6...................... (i)

16p + q = 20 .................(ii)

Subtracting equation (i) from equation (ii), we have;

(16p-9q) + (q-q) = 20-6

7p + 14

p=2

Substituting p = 2 into equation (i)

9p + q = 6

9(2) + q = 6

18 + q = 6

q = 6 - 18

q = -12

Hence, p = 2 and q = -12

(ii) The equation for the given table of values

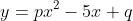  becomes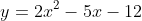  

ANSWER