WAEC Mathematics Question 2015 ( Essay Question Nine 9)

May 26, 2020

By Kings

0 Comments

QUESTION 9

(a) The first term of an Arithmetic Progression (AP) is 8, the ratio of the 7th term to the 9th term is 5 : 8, find the common difference of the AP.

(b) A trader bought 30 baskets of pawpaw and 100 baskets of mangoes for N2,450.00. She sold the pawpaw at a profit of 40% and the mangoes at a profit of 30%. If her profit on the entire transaction was N855.00, find the;

(i) cost price of a basket of pawpaw ;

(ii) selling price of the 100 baskets of mangoes.

Solution

(a) Given that the first term = a = 8,

ratio of 7th to 9th term = 5:8 and

common difference , d = ?

Using Un = a + (n-1)d

Where;

n=Number of terms

a = First term

d = Common difference.

The 7th term

$U_{7}=8+(7-1)d$

$U_{7}=8+6d$ ..........................(i)

The 9th term

$U_{9}=8+(9-1)d$

$U_{9}=8+8d$ ..........................(ii)

The ratio of 7th to 9th term;

ie. $U_{7}:U_{9}$ = 5:8

$\therefore \frac{8+6d}{8+8d}=\frac{5}{8}$

Cross multiplying, we have

8(8 + 6d) = 5(8 + 8d)

64 + 48d = 40 + 40d

Collecting liketerms, we have,

48d - 40d = 40 - 64

8d = -24

d = -3

(b) Let the cost price for pawpaw = p and mango = m

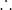
$\therefore$ 30 baskets of pawpaw = 30 x p = 30p

100 baskets of mangos = 100 x p = 100m

Sum of the fruits = ₦2,450

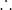
$\therefore$ 30p + 100m = ₦2,450

dividing through by 10, we have;

3p + 10m = 245................(i)

Note: She sold the pawpaw at a profit of 40%. ie.

$30p \times \frac{40}{100}$

$30p \times \frac{40}{100}= 12p$

Hence, her profit for selling 30 baskets of pawpaw = 12p

Also she sold the mangoes at a profit of 30%. ie.

$100m \times \frac{30}{100}$

$100 \times \frac{30}{100}=30m$

Hence, her profit for selling 100 basketsof mangoes = 30m

But her profit on the entire transaction(sum) = ₦855

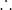
$\therefore$ 12p + 30m = 855

Dividing through by 3, we have,

4p + 10m = 245.....................(ii)

Solving equation (i) and (ii) simultaniously, we have,

3p + 10m = 245......................(i)

4p + 10m = 285 .....................(ii)

Sbtracting equation (i) from (ii)

(4p - 3p) + (10m - 10m) = 285 - 245

p + 0 = 40

p = 40

Hence, the cost price for a basket of pawpaw(p) = ₦40.00

(ii) Selling price for 100 baskets of mangoes.

First we solve for the cost price for a basket of mango by substitutung p = 40 into equation (i)

3p + 10m = 245

3(40) + 10m = 245

120 + 10m = 245

10m = 245 -120

10m = 125

$\therefore m =\frac{125}{10}$

m = ₦12.50

Hence, coat price for 100 baskets of mangoes = 100 x 12.5

= ₦1,250

Note: She made a profit of 30% for selling 100 baskets of mangoes,

$\frac{SP-CP}{CP}\times \frac{100%}{1} = % Profit$

Where, SP = Selling price

CP = Cost price

$\therefore \frac{SP-1250}{1250}\times \frac{100%}{1} = 30%$

$\therefore \frac{SP-1250}{1250}=\frac{30}{100}$

$\frac{SP-1250}{1250}=\frac{3}{10}$

Cross multiplying, we have;

10(SP - 1250) = 3 x 1250

10SP - 12500 = 3750

10SP = 3750 + 12500

10SP = 16250

$SP= \frac{16250}{10}=\frac{1625}{1}$

SP = 1625

SP = ₦1625

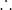
$\therefore$ The selling price for 100 baskets of mangoes = ₦1625

0 Comments:

WAEC Mathematics Question 2015 ( Essay Question Six 6b )

May 24, 2020

By Kings

0 Comments

QUESTION 6b

(b) The cost (c) of producing n bricks is the sum of a fixed amount, h, and a variable amount, y, where y varies directly as n. If it costs GH¢950.00 to produce 600 bricks and GH¢ 1,030.00 to produce 1000 bricks,

(i) Find the relationship between c, h and n ;

(ii) Calculate the cost of producing 500 bricks.

SOLUTION

From the statement, we have

where K is constant

Substituting y = Kn into the equation we have;

c = h + Kn ........................(i)

Where c = 950 , n = 600

$\therefore$ 950 = h + 600K ....................(a)

Also, where c = 1030, n = 1000

We have 1030 = h + 1000K .................(b)

Solving equation (a) and equation (b) simutaniously

950 = h + 600K ...................(a)

1030=h + 1000K..................(b)

Subtracting equation (a) from equation (b)

(1030-950) = (h-h) + (1000K-600K)

80= 400K

$K = \frac{80}{400}$

$K = \frac{1}{5}$

Substituting $K = \frac{1}{5}$ into equation (a) , we have;

$950 = h +600(\frac{1}{5})$

When 5 goes into 600 we will have 120,

So, therefore

950 = h + 120

h = 950-120

h = 830

Hence;

(i) To obtain the relationship between c, h and n, we have

c = h + Kn

$c = 830 \frac{1}{5}n$ $\therefore$

$\therefore c=830 + \frac{n}{5}$ Answer

(ii) The cost of producing 500 bricks

ie. n = 500

Given

$c=830 + \frac{n}{5}$

$c=830 + \frac{500}{5}$

(500 divided by 55 gives us 100)

So therefore,

c = 830 + 100

c = GH¢ 930 ANSWER

Download it to your device using the links below

Download link 1

Download Link 2

Download Link 3

0 Comments:

WAEC Mathematics Question 2015 ( Essay Question Five 5 )

May 23, 2020

By Kings

WAEC Mathematics 2015, WAEC Mathematics 2015 Essay

0 Comments

Question 5

A trapezium PQRS is such that PQ // RS and the perpendicular P to RS is 40 cm. If |PQ| = 20 cm, |SP| = 50cm and |SR| = 60 cm. Calculate, correct to 2 significant figures, the;

(a) Area of the trapezium ;

(b) < QRS.