Find the derivatives of Y = ( X +5 )( X2 - 6X )

Find the derivatives of Y = (X +5)(X² - 6X)

SOLUTION

Y = (X +5)(X² - 6X)

Applying the product rule of Indices

dy dx = Udv dx + Vdu dx

Where, U = X+5 and V = X²-6X

So therefore, du dx = 1 and dv dx = 2X-6

Therefore: dy dx = (X+5)(2X-6) + (X² - 6X)1

Lets expand the bracket.

(X+5)(2X-6) = X(2X-6)+5(2X-6)

2X²-6X+10X -30

2X²+4X-30

3X² - 2X - 30

So Therefore, dy dx = 3X²-2X-30

Read more

Find the derivatives of Y = 8X4 + 16X3 - 4X2 + X - 20

Question 1 :Y = 8X⁴ + 16X³ - 4X² + X - 20

SOLUTION

Y = 8X⁴ + 16X³ - 4X² + X - 20

Recall that Xⁿ = nX^n-1

So therefore: dy dx = 4(8)X^4-1 + 3(16)X^3-1 - 2(4)X^2-1 + X^1-1 - 0

dy dx = 32X³ + 48X² - 8X + 1

Read more

WAEC Mathematics Question 2015 ( Essay Question Seven 7)

QUESTION 7

The table is for the relation 

(a)(i) Use the table to find the values of p and q.

(ii) Copy and complete the table.

(b) Using scales of 2cm to 1 unit on the x- axis and 2 cm to 5 units on the y- axis, draw the graph of the relation for −3≤x≤5$-3\le x\le 5$.

(c) Use the graph to find : 

(i) y when x = 1.8  ; (ii) x when y = -8.

SOLUTION

a(i) To find the value of p and q from the given table of values when x = -3, y= 21

and when x = 4, y = 0.

So considering s = -3 and y = 21 using the givem equation .

Substituting the vale of x and y  into the equation, we have;

21 =9p + 15 +q

21-15 = 9p + q

6 = 9p +q

9p +q = 6...................... (i)

Also, when x = 4 and y = 0

Substituting into the equation 

Substituting the vale of x and y  into the equation, we have;

0 = 16p - 20 + q

0 + 20 = 16p + q

20 = 16p + q

16p + q = 20 .......................(ii)

Solving equation (i) and (ii) simultaneously ,

6 = 9p +q ......................... (i)

20 = 16p + q.....................(ii)

9p +q = 6...................... (i)

16p + q = 20 .................(ii)

Subtracting equation (i) from equation (ii), we have;

(16p-9q) + (q-q) = 20-6

7p + 14

p=2

Substituting p = 2 into equation (i)

9p + q = 6

9(2) + q = 6

18 + q = 6

q = 6 - 18

q = -12

Hence, p = 2 and q = -12

(ii) The equation for the given table of values

  becomes  

ANSWER

Read more

INDICES

Definition of Indices

Indices or Index(singular) deals with numbers raised to some powers, example: X² which we call X raised to the power of 2.
In the above example, X is the Base while "²" is the power or index or quotient.
Indices can also be called Exponents.

Laws of Indices

1. Multiplication Law of Indices Says: X^a x X^b = X^a+b
2. Division Law of Indices Says: X^a÷ X^b or X^a X^b = X^a-b
3. Power of Zero Law of Indices Says: X⁰= 1
4. Negative Power Law of Indices Says: X^-a = 1 X^a
5. Bracket Law of Indices Says: (X^a)^b = X^{a x b}
6. Fractional Power Law of Indices Says: X ^{a b} = (^b√X)^a

Question 1

If 27^x x 3^1-x 9^2x = 1 , Find x

WAEC 2015

SOLUTION

Lets rewrite the question

27^x x 3^1-x 9^2x

We have to first take the LHS to the same base

27 = 3 x 3 x3 = 3³

9 = 3 x 3 = 3²

3 = 3 = 3

So,

3^3(x) x 3^(1-x) 3^2(2x) = 1

3^3x x 3^1-x 3^4x = 1

From the multiplication Law of Indices, we will add the powers,

3^{3x + (1-x)} 3^4x = 1

3^{3x + 1-x} 3^4x = 1

Collecting Live terms of the powers.

3^{2x + 1} 3^4x = 1

We then have to apply the division Law of Indices, By this we mean to subtract the powers of the denominator since its same base (3).

3^{2x + 1 - (4x)} = 1

Then we expand the bracket, we have

3^{2x + 1 -4x} = 1

Collect the like terms, we have

3^{-2x + 1} = 1

Then we apply the zero law to the RHS
Recall that anything raise to power of zero is 1.

3^{-2x + 1} = 3⁰

Equating the powers

-2𝑥+1 = 0

Collecting like terms
-2𝑥 = 0 - 1
-2𝑥 = - 1
Hence we have - on both side, we take care of it.
Making the equation 2𝑥 = 1
Then making 𝑥 the subject of the formular,
We have
𝑥 = 1 2 Answer

Read more

WAEC Mathematics Question 2015 ( Essay Question Ten 10)

QUESTION 10

10(a)without using mathematical tables or calculators;

Simplify: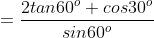 

10(b)From an aeroplane in the air at a horizontal distance of 1050m, the angle of depression of the base of a control tower at an instance are 36 and 41 respectively.

Calculate, correct to the nearest meter, the;

(i)                 Height of the control tower.

(ii)               Shortest distance between the aeroplane and the base of the control tower.

 

Solution

10a. We solve using equilateral triangle

Dividing the triangle into two equal parts.

Note: BC = BD + CD

Where;

BD = CD

BC = 2

So therefore, 2 = CD + CD

2 = 2CD

CD =  = 1

We solve for the unknown side (AD) by applying Pythagoras theorem.

|AC|²= |AD|² + |CD|²

|AD|²= |AC|² - |CD|²

|AD|²= 2² - 1²

|AD|²= 4 - 1

|AD|²= 3

AD =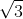 

 The diagram becomes

From the above diagram, we consider SOHCAHTOA

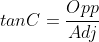
tan60 =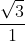 

tan60 =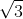 

 

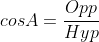
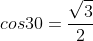
 Also, 

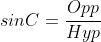
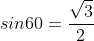
Substituting the value of tan60, cos30 and sin60 into the equation 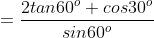  respectively,

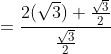
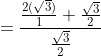
The LCM of the numerator is 2

 

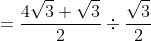
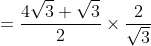
= 5 ANSWER

 

 

10b.

Central Tower

Let the height of the tower be h1 and the distance between the top of the central tower and the horizontal distance of the aeroplane, be h2. Hence, total distance from the base of the central tower and the base of the aeroplane be h.

So therefore, h = h1 + h2

To solve for h1, we consider      ABD and apply SOHCAHTOA

Using tanA =

tan36 =

h1 = 1050tan36

h1 = 762.9m

Also, to solve for h, ie. h1 + h2, we consider    ABC

Using tanA =

tan41 =

h = 1050tan41

So therefore, h = 912.8m

Hence, the height of the central tower h2 can be calculated using the formula

h = h1 + h2

h2 = h – h1

h2 = 912.8 – 762.9

h2 = 149.9m

Note: The shortest distance between the aeroplane and the base of the control tower is the distance between AC

cosA =

cosA =

AC =

AC = 1391.3m

Read more